你是否想过“无中生有”,让一切仅存于想象的灵感巧妙地实现?数百年间无数物理学家投身于此,建立起无生命物质世界的第一原理框架——量子力学与统计力学。在21世纪的今天,借助高度发展的数理理论与发达的计算机技术,“无中生有”似乎不再是空中楼阁。
1.你见过百发百中的篮板吗?
你见过这样的篮板吗?不论你从哪个角度投球,都能百发百中。听起来匪夷所思,但设计者从“建立一个模型让所有可能角度的进球路线都变得合理”的想法出发,最终实现了这个天马行空的计划。
试着想想,假如通过传统的投球实验测量数据来调整篮板的模型,工作量和时间成本十分庞大,还无法排除无关变量影响。面对庞大且重复的工作量,正是让计算机模拟大放异彩的时刻。作者采用蒙特卡洛模拟方法进行暴力求解,让计算机代替人来重复上千万次的投球采样,再运用最小二乘法对不同角度和坐标的数据进行拟合获得理想的篮板形状,导出数控机床的生成路径,最终通过数控机床实现理论模型。在这个过程中,正是计算机模拟让百发百中的篮板不再是天方夜谭般的存在。
那么在软物质材料设计中,我们能否运用如今成熟的计算机模拟使得分子合理存在呢?作为一项集物理原理、数学建模、计算机高性能运算三位一体从而预测分子动力学行为与热力学性质的新兴技术,分子模拟(Molecular Simulation)给了我们答案。得益于分子模拟理论、方法以及计算机技术的发展,分子模拟已经成为继实验和理论手段之后,从分子水平了解和认识世界的第三种手段[1]。它是理论的延伸,又是架向实验的桥梁。对于很多分子体系结构和性质的研究目前不仅可以通过实验来实现,还可以通过分子模拟来展开。分子模拟除了能帮助我们理解实验现象,还能发现或者预测新的物理现象。
随着计算机技术的飞速发展与物理理论的逐渐完善,分子模拟从最初的小尺度简单模型模拟,成长为如今能够快速并行计算大尺度复杂模型的模拟。这个过程有着无数科学家在其中潜心钻研,在分子模拟的银河中留下了一颗又一颗璀璨的星。
2.分子模拟发展历史
20世纪初,电子计算机的发明揭开了信息时代的序幕;20世纪中页,晶体管取代真空管使得计算机性能大幅提升,分子模拟也在此时初现端倪。
1953年,Metropolis等人采用蒙特卡罗(Monte Carlo, MC)方法模拟了2D球形致密流体体系。这在分子模拟史上是开天辟地的大事件。
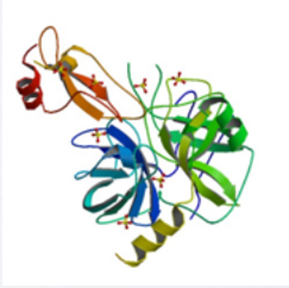
1957年,Alder和Wainwright首次采用分子动力学(Molecular Dynamics, MD)方法,模拟研究了硬球流体之间的相互作用,见图1。有关简单液体行为的许多重要见解都来自他们的研究。
1964年,Rahman采用分子动力学方法首次模拟了液氩的相互作用。
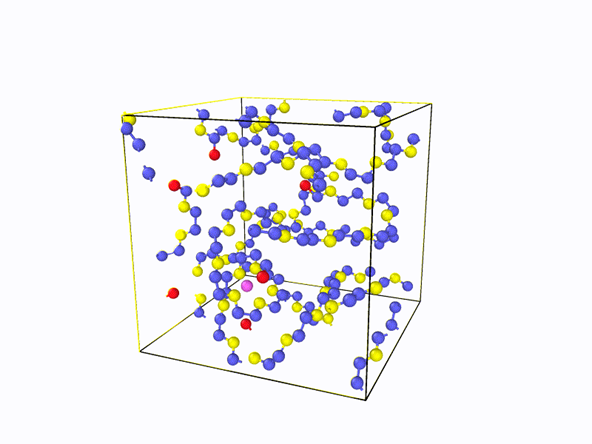
1969年,Barker和Watts采用蒙特卡罗方法模拟了水分子。
1974年,Rahman和Stillinger同样模拟了水分子体系,见图2,但使用的方法是分子动力学。
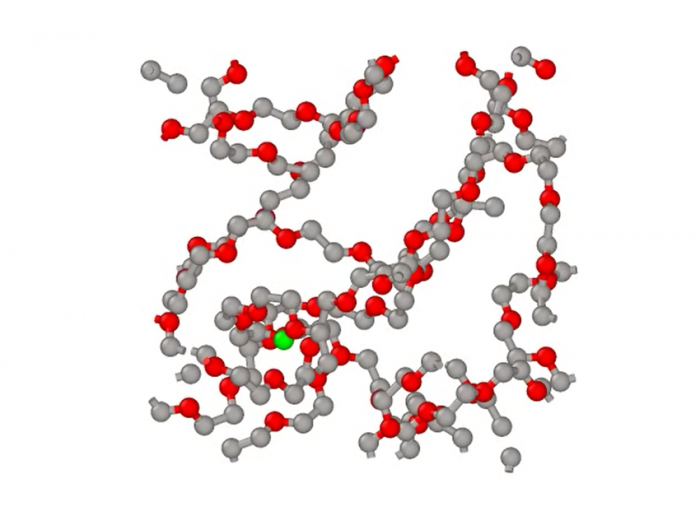
1977年,McCammon 等人应用分子动力学方法,首次进行了BPTI蛋白酶的模拟。模拟时间达到了皮秒级别。
1986年,R.Car和M.Parrinello开发了基于量子力学的从头算分子动力学(ab initio MD)。
1994年,York等人模拟水合BPTI蛋白酶的时间达到纳秒级别。
……
图1 硬球流体的相互作用
图2 使用分子动力学模拟水分子体系 图3 使用分子动力学模拟BPTI
图4 四种状态下的LJ硬球模型(A:气态 B:不稳态 C:液态 D:固态)
随着计算机技术的飞速发展,算法和力场日益完善,分子模拟的效率和精度获得极大提高,已能够广泛应用于多个学科领域:
在药物设计领域,可用于研究病毒、药物的作用机理等;在生物科学领域,可用于表征蛋白质的多级结构与性质等;在材料学领域,可用于研究结构与力学性能、材料的优化设计等;在化学、化工领域,可用于研究表面催化及机理,构建和表征高分子链以及晶态或非晶态本体聚合物的结构,预测包括共混行为、扩散、内聚与润湿以及表面粘接等重要性质。
分子模拟的应用当然远不止这些,在此也不能一一列举。重要的是,我们该如何进行分子模拟呢?
3.分子模拟步骤简要介绍
分子模拟(Molecular Simulation)是一类通过计算机模拟来研究分子或分子体系结构与性质的重要研究方法[1],主要包括分子动力学(Molecular Dynamics, MD)方法和蒙特卡罗(Monte Carlo, MC)方法。前者是通过体系中分子坐标的变化来计算分子之间的相互作用力,该方法主要依靠牛顿力学来模拟分子体系的运动,再从体系的不同状态构成的系统中抽取样本,计算体系的构型积分,并以此为基础进一步计算体系的热力学量和其他宏观性质。与蒙特卡罗模拟方法不同的是,分子动力学始终受时间控制[2]。
蒙特卡罗方法又称为计算机随机模拟方法,是一种依赖于重复随机抽样来获得数值结果的数值计算方法,主要基于概率论、统计力学和系综理论。蒙特卡罗获得新构象的过程如下:首先随机产生一个尝试构象;通过计算构象的能量得到一个概率因子;最后将概率因子与产生的随机数进行比较,按照一定的规则,接受或拒绝这个尝试构象,完成一次循环[3]。
与分子动力学相比,蒙特卡罗方法有时更为简单和高效。二者最大的区别在于分子动力学主要是通过分子间作用力促使体系变化,而蒙特卡罗方法则是通过不同构象之间的能量差异完成构象的更迭。选择哪一种方法依赖于具体研究的体系性质,例如,若想得到体系的含时动力学性质,分子动力学是最好的选择;而蒙特卡罗方法更适合在非含时的统计平均计算方法领域,但它无法得到系统的动态信息[2]。
模拟与理论、实验相互补充,彼此验证。从下图中可以看出,模拟可视作理论和实验的桥梁。对于理论研究而言,模拟可以为理论研究提供数据进行复杂数值解的方法和手段[4];对于实验研究而言,模拟可以对实验数据进行分析,并获得实验反应细节。三者关系相辅相成,相得益彰。
图5 分子模拟、理论、实验三者关系图
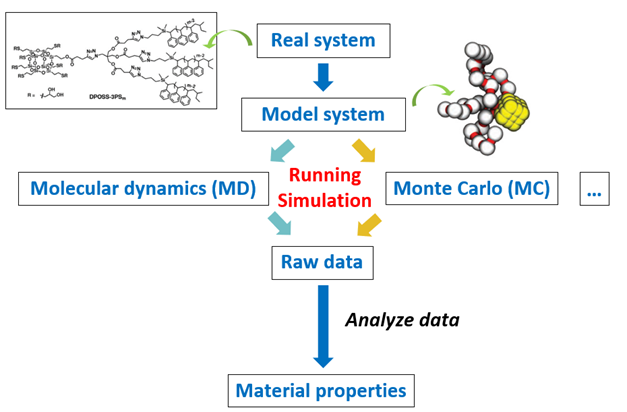
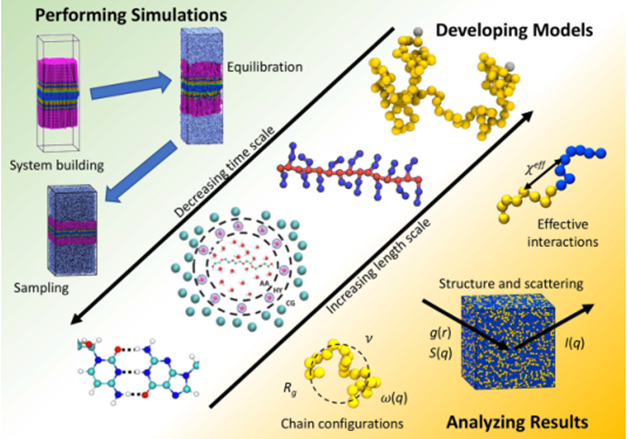
分子模拟的主要步骤包括选定真实体系、建立模型、运行模拟和分析数据,见图6,图7。首先根据真实体系建立模型,根据不同的尺度采用适合的模型,常用的模型有全原子模型和粗粒化模型;接着进行分子模拟;模拟结束后再对数据结果进行分析,进而得到其相结构和热力学性质等信息。
图6 模拟工作的流程
图7 聚合物模拟关键步骤[5]
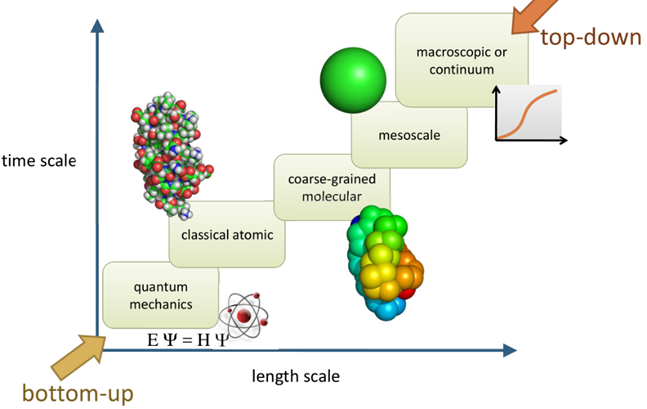
为了模拟分子体系在极大的时空跨度内的结构与性质,在不同的时空尺度下应采用不同的模型,见表1.
表1 各种物理体系的特征时空尺度与模拟方法[1]

图8 不同尺度下的模拟
全原子分子动力学模拟的基本思想就是将体系的每个原子当作一个小球,然后求解体系的牛顿运动方程。计算体系的总势能是至关重要的一步,力场就是体系原子之间相互作用势能函数的综合表达式,包括了原子或分子间的键相互作用和非键相互作用以及约束项。其中,键相互作用又包括了键与键之间的伸缩势能、键角的弯曲势能以及二面角的势能等,而非成键相互作用主要是指范德瓦尔斯相互作用能和库伦静电相互作用势能[6]。图12为锂离子在聚合物体系中进行扩散运动的全原子模拟。全原子模拟具有更高精度,可以更好的描述分子体系的结构与性质,但计算量大,可模拟的时间和空间尺度有限[1]。
在现有的计算速度下,微观尺度上的全原子分子动力学模拟能够描述的体系尺寸通常仅有几十埃。显然,描述原子细节的全原子模型由于自由度过多,当计算资源受限时,必须减小模拟体系规模或缩短体系的演化时间,否则将会影响模拟效果。因此必须建立从微观到介观的衔接,构建能在介观尺度上进行有效分子模拟的粗粒化模型[4]。
在软物质科学领域,很多物理现象都伴随着发生在原子尺度上的过程,而这能够直接影响到介观尺度上的结构和动力学性质。因此,采用分子模拟方法定量研究高分子体系物理化学性质,建立衔接到微观尺度的粗粒化模型变得越来越重要。通常,针对具体研究的体系,需要构建不同的粗粒化模型[4]。聚合物链的粗粒化过程就是通过整合链上大量微观细节,将聚合物分子描述成由不同柔性弹簧连接的粗粒化粒子组成的链,并用经验势或精确的势来描述分子间的相互作用。图11为使用粗粒化模型对纳米粒子球的表面引发的链增长聚合反应进行模拟。实际上,无论选择哪种粗粒化方法和非键相互作用势函数形式,粗粒化的基本要义都是在能够重复尽量多的真实体系性质的前提下,采用尽量简单的势函数形式。
图9 PE分子链的粗粒化模型和力场示意图[7]
图10 聚苯乙烯的粗粒化示意图[8]
采用特定的粗粒化模型来研究,一方面由于忽略了很多不必要的细节,加快了体系的动力学过程;另一方面由于采用了合适尺度的模型,减少了整个体系演化所需要的时间。在分子链的特定粗粒化模型中,每个粗粒化粒子可以代表几个原子、几个单体甚至分子片段。由于粗粒化粒子间势函数比全原子的软,所以即使采用较大的时间步长,粗粒化模拟的运行也很稳定。通常粗粒化模拟的计算效率较全原子模拟的至少要提高3到4个数量级。目前,具有最高简化程度、最少自由度的分子模型就是粗粒化模型[1]。
图11 模拟纳米粒子的表面引发的链增长聚合反应[9]
图12 锂离子在聚合物中的扩散运动
图13 锂离子在聚合物中的扩散运动
分子模拟作为一种研究分子体系结构与性质的计算方法,已被广泛用于化学化工、生物医药、材料科学与工程、物理等学科领域。其最直接的研究结果包括分子体系的结构特征、各种热力学性质、体系的各种迁移性质等。总的来说,达到更高的效率、模拟更大的体系、实现更长的演化时间、取得更精确的模拟结果是分子模拟未来的发展趋势。
参考文献
- 严六明,朱素华.分子动力学模拟的理论与实践[M].科学出版社:北京,2013:1.
- 苑世领,张恒,张冬菊.分子模拟理论与实验[M].化学工业出版社:北京,2016:3.
- 苑世领,张恒,张冬菊.分子模拟理论与实验[M].化学工业出版社:北京,2016:110.
- 郭洪霞.高分子粗粒化分子动力学模拟进展[J].高分子通报,2011(10):154-163.
- Thomas E. Gartner, Arthi Jayaraman.Modeling and Simulations of Polymers: A Roadmap[J].Macromolecules,2019,52(52):755-786.
- 熊开欣. 基于Amber bsc1和bsc0力场的DNA柔性的全原子分子动力学模拟研究[D].武汉大学,2018.
- 蔡庄立. 聚乙烯材料导热性能的粗粒化分子模拟研究[D].东南大学,2019.
- 朱有亮. 实现更大空间及时间尺度聚合物模拟的一些探索[D].吉林大学,2013.
- Hong Liu,You-Liang Zhu, Jing Zhang,etc.Influence of Grafting Surface Curvature on Chain Polydispersity and Molecular Weight in Concave Surface-Initiated Polymerization[J].ACS Macro Letters,2012,1(1):1249-1253.
本文作者为华南软物质科学与技术高等研究院19级硕士生罗煜林、黄崇洋和20级硕士生杨紫琼,指导老师为华南软物质科学与技术高等研究院张睿研究员。张睿课题组的研究领域为软物质理论计算与模拟,主要关注:(1)巨型分子的多级组装结构与动力学演变;(2)高分子复合材料中的协同动力学过程;(3)超分子溶液中的自组装与仿生现象;(4)软物质中的玻璃化转变。目前在软物质科学与工程专业招收学术博士及硕士;在软物质多尺度理论模拟、基于机器学习的软物质材料优化、非平衡统计力学理论发展与应用方向上招聘博士后。